Welcome!
I am an Assistant Professor at the IMDEA Software Institute. Previously, I was a Research Associate in the Automated Verification Group of the University of Oxford. I hold a PhD degree from ENS Paris-Saclay, where I was a student of Stéphane Demri and Étienne Lozes in the Laboratoire Spécification et Vérification.
Below, you will find a summary of current and past projects. All my papers are available here.
Non-linear Existential Arithmetic Theories
Integer programming is the problem of finding an (optimal) solution to a system of linear inequalities over the integers. Feasibility of such systems can be solved in NP, practical algorithms exists and are routinely used to solve scheduling and network problems. Several non-linear extensions of integer programming are known to be decidable, but their computational complexity is unknown and algorithms are largely unrefined. This project aims at tackling these problems, providing novel algorithms and complexity results for systems of inequalities featuring exponentiation, divisibility, and other non-linear operations.
Advanced Reasoning in Arithmetic Theories
The goal of the ERC project ARiAT is to advance the state-of-the-art in decision procedures for first-order arithmetic theories, improve complexity bounds and push the decidability frontier of extensions of arithmetic theories with counting and non-linear operations. See here for more information.
- On Polynomial-Time Decidability of k-Negations Fragments of FO Theories (MFCS'23)
- Geometric decision procedures and the VC dimension of linear arithmetic theories (LICS'22)
- Higher-Order Quantified Boolean Satisfiability (MFCS'22)
-
Quantifier elimination for counting extensions of
Presburger arithmetic
(FOSSACS'22) - On deciding linear arithmetic constraints over p-adic integers for all primes (MFCS'21)
Reachability Predicates in Separation Logic
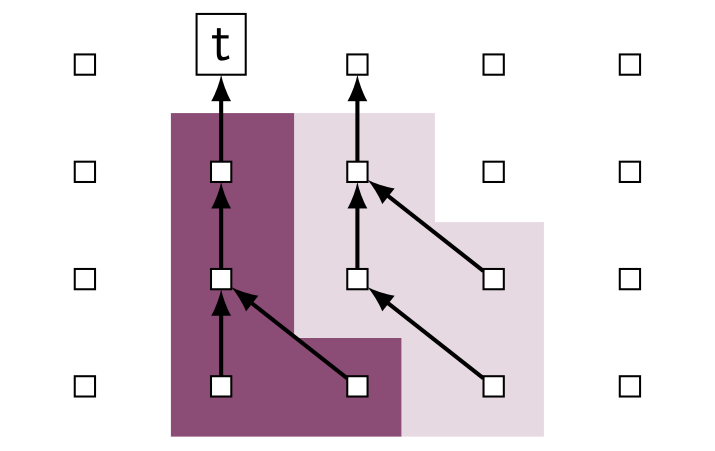
The goal of this project is to study the complexity and expressiveness of separation logics featuring reachability predicates. Separation logic is a mathematical formalism for reasoning about pointer programs. Among the various features of this logic, reachability predicates have a special status, as they allow to express crucial properties of the memory such as acyclicity and garbage-freedom.
-
The effects of adding reachability predicates in quantifier-free separation logic
(TOCL'21 and FOSSACS'18) - An auxiliary logic on trees (I&C'22 and FOSSACS'20)
- Extending propositional separation logic for robustness properties (FSTTCS'18)
Modal Logics with Composition Operators
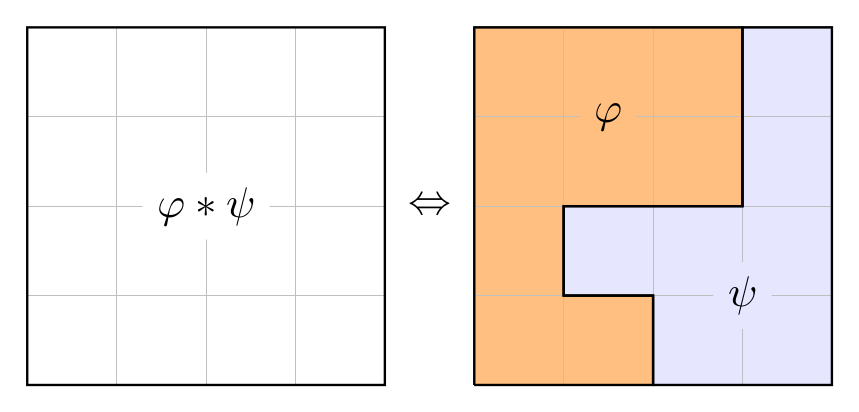
The goal of this project is to develop a framework of modal logics featuring different forms of frame composition that are heavily inspired by the logic of Bunched Implications. By relying on standard techniques from finite model theory, we study the expressiveness and computational complexity of our logics, and compare them with more standard formalisms (e.g. graded modal logic).
-
On composing finite forests with modal logics
(TOCL'23 and LICS'20, ) - Modal logics and local quantifiers: a zoo in the elementary hierarchy (FOSSACS'22)
- A framework for reasoning about dynamic axioms in description logics (IJCAI'20)
Internal Calculi for Spatial Logics
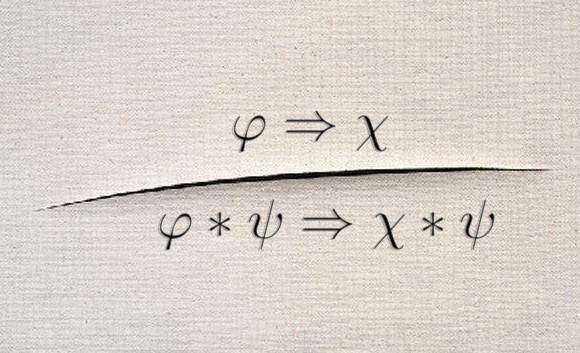
The goal of this project is to design internal axiomatisations for spatial logics such as separation logics and ambient logics. Designing an internal (a.k.a. Hilbert-style) axiomatisation for your favourite logic is usually quite challenging. It does not lead necessarily to optimal decision procedures, but the completeness proof usually provides essential insights to better understand the logic at hand, and develop better abstractions that can improve the performances of tools.
- A complete axiomatisation for quantifier-free separation logic (LMCS'21)
-
Internal proof calculi for modal logics with separating conjunction
(JLC'21 and JELIA'19) - Internal calculi for separation logics (CSL'20)